A boxplot (, ) (also
known as a box-and-whisker plot) provides a graphical overview of how data is distributed
over the number line. Rattle's Box Plot displays a graphical
representation of the textual summary of data. It is
useful for quickly ascertaining the skewness of the distribution of
the data. If we have identified a Target variable, then the boxplot
will also show the distribution of the values of the variable
partitioned by values of the target variable, as we illustrate for the
variable Age where Adjusted has been chosen as the Target variable.
The boxplot (which here is shown with the Annotate option checked)
shows the median
(which is also called the second
quartile
or the 50th percentile) as the
thicker line within the box (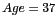 over the whole population, as we
can see from the Summary option's Summary check
box). The top and bottom extents of the box (
over the whole population, as we
can see from the Summary option's Summary check
box). The top and bottom extents of the box (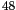 and
and 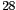 respectively) identify the upper quartile (the third quartile or the
75th percentile) and the lower quartile (the first quartile and the
25th percentile). The extent of the box is known as the
interquartile range
(
respectively) identify the upper quartile (the third quartile or the
75th percentile) and the lower quartile (the first quartile and the
25th percentile). The extent of the box is known as the
interquartile range
( ). The
dashed lines extend to the maximum and minimum data points that are no
more than
). The
dashed lines extend to the maximum and minimum data points that are no
more than 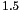 times the interquartile range from the
median. Outliers (points further than
times the interquartile range from the
median. Outliers (points further than 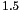 times the interquartile
range from the median) are then individually plotted (at 79, 81, 82,
83, and 90). The mean
(38.62) is also displayed as the
asterisk.
times the interquartile
range from the median) are then individually plotted (at 79, 81, 82,
83, and 90). The mean
(38.62) is also displayed as the
asterisk.
The notches in the box, around the median, indicate a level of
confidence about the value of the median for the population in
general. It is useful in comparing the distributions, and in this
instance it allows us to say that all three distributions being
presented here have significantly different means. In particular we
can state that the positive cases (where  ) are older than
the negative cases (where
) are older than
the negative cases (where 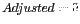 ).
).
We note that the annotated box plot (as enable by checking the
Annotate check box) does not attempt to place the
annotations in any particularly optimal location, except a little
below the point being annotated. They may be a little difficult to
read at times. The user is at liberty to correct thus through
replicating the plotting steps from the log window, but modifying the
offsets in the display of the annotations.
Copyright © Togaware Pty Ltd
Support further development through the purchase of the PDF version of the book.
The PDF version is a formatted comprehensive draft book (with over 800 pages).
Brought to you by Togaware. This page generated: Sunday, 22 August 2010




![]() ) are older than
the negative cases (where
) are older than
the negative cases (where ![]() ).
).