
Desktop Survival Guide
by Graham Williams


|
DATA MINING
Desktop Survival Guide by Graham Williams |

|
|||
|
Todo: ABS Example of fitting linear model but no kernel for job category classification from a text description.
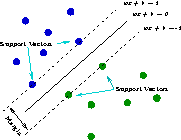
A Support Vector Machine (SVM) searches for so called support vectors which are data points that are found to lie at the edge of an area in space which is a boundary from one class of points to another. In the terminology of SVM we talk about the space between regions containing data points in different classes as being the margin between those classes. The support vectors are used to identify a hyperplane (when we are talking about many dimensions in the data, or a line if we were talking about only two dimensional data) that separates the classes. Essentially, the maximum margin between the separable classes is found. An advantage of the method is that the modelling only deals with these support vectors, rather than the whole training dataset, and so the size of the training set is not usually an issue. If the data is not linearly separable, then kernels are used to map the data into higher dimensions so that the classes are linearly separable. Also, Support Vector Machines have been found to perform well on problems that are non-linear, sparse, and high dimensional. A disadvantage is that the algorithm is sensitive to the choice of variable settings, making it harder to use, and time consuming to identify the best.
Support vector machines do not predict probabilities but rather produce normalised distances to the decision boundary. A common approach to transforming these decisions to probabilities is by passing them through a sigmoid function.
c("0"=4, "1"=1) resulted in the best risk chart. For a
50% caseload we are recovering 94% of the adjustments and 96% of
the revenue.
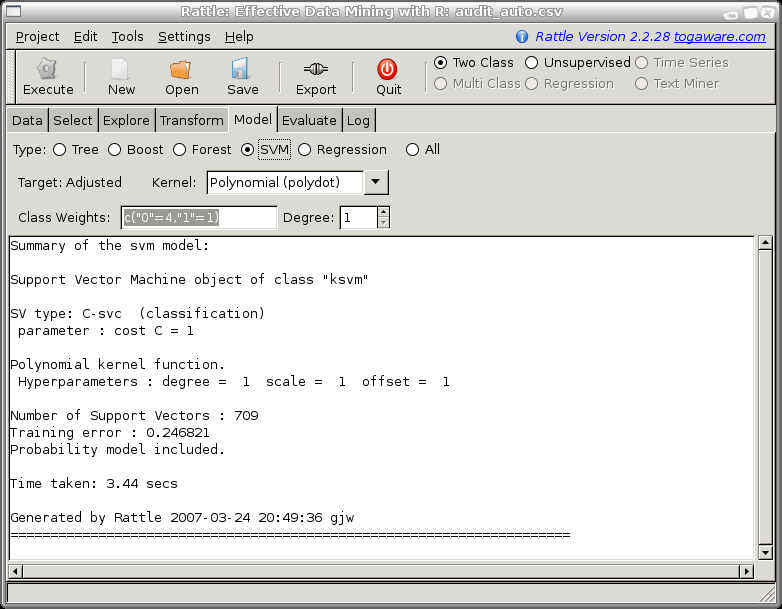
There are other general variables that can be set for ksvm, including the cost of constraint violation (the trade-off between the training error and margin? could be from 1 to 1000, and is 1 by default).
For best results it is often a good idea to scale the numeric variables to have a mean of 0 and a standard deviation of 1.
For polynominal kernels you can choose the degree of the polynomial. The default is 1. For the audit data as you increase the degree the model gets much more accurate on the training data but the model generalises less well, as exhibited by its performance on the test dataset.
Another variable often needing setting for a radial basis function
kernel is the sigma value. Rattle uses automatic sigma estimation
(sigest) for this kernel, to find the best sigma, and so the user need
not set a sigma value. If we wanted to experiment with various sigma
values we can copy the R code from the Log tab and paste
it into the R console, add in the additional settings, and run the
model. Assuming the results are assigned into the variable
crs$ksvm, as in the Log, we can the evaluate the perfromance of
this new model using the Evaluate tab.