
Desktop Survival Guide
by Graham Williams


|
DATA MINING
Desktop Survival Guide by Graham Williams |

|
|||
Descriptive Analysis |
The function survfit fits a survival curve for censored data. The default is to use the Kaplan-Meier method.
See help on survfit.formula for a discussion on Kaplan-Meier, Fleming-Harrington, Kalbfleisch-Prentice, Tsiatis/Link/Breslow. Essentially the estimates based on Kalbfleisch-Prentice and the Tsiatis/Link/Breslow reduce to the Kaplan-Meier and Fleming-Harrington estimates, respectively, when the weights are unity (as I think they are unless we specifically set them in the function call).
We first look at the simple dataset. We can fit a single survival curve by using 1 as the right hand side of the formula. The table and the plot contain a 95% confident interval.
> s.survfit <- survfit(s.Surv ~ 1, data=simple) > summary(s.survfit) |
Call: survfit(formula = s.Surv ~ 1, data = simple)
time n.risk n.event survival std.err lower 95% CI
2 9 1 0.889 0.105 0.7056
7 4 1 0.667 0.208 0.3618
9 3 1 0.444 0.228 0.1624
10 2 1 0.222 0.194 0.0401
upper 95% CI
1
1
1
1
|
> plot(s.survfit, xlab="Time", ylab="Survival Probability", col=3) |
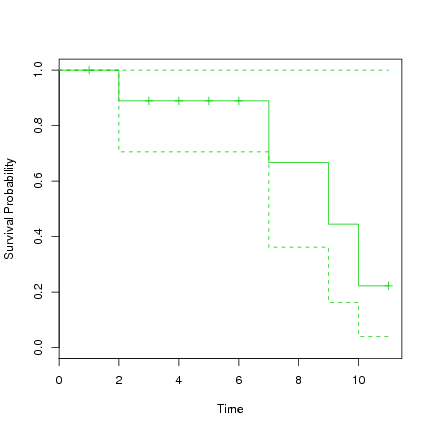
The first known death is at time 2, at which time 90% are surviving. From this time to time 7 these 90% survive to at least time 7 when the next death occurs. From this time the model suggests 72% remain alive. They remain alive until time 9 at which time 48% remain alive. And so on. Note the confidence interval around these survival rates, which range quite widely up to 100%. With such a small dataset we don't expect too much accuracy on the fit.
For the lung dataset we fit a survival curve and plot it.
> l.survfit <- survfit(l.Surv ~ 1, data=lung)
> plot(l.survfit, xlab="Survival Time in Days", ylab="% Surviving", col=3,
yscale=100, main="Survival Distribution (Overall)")
|
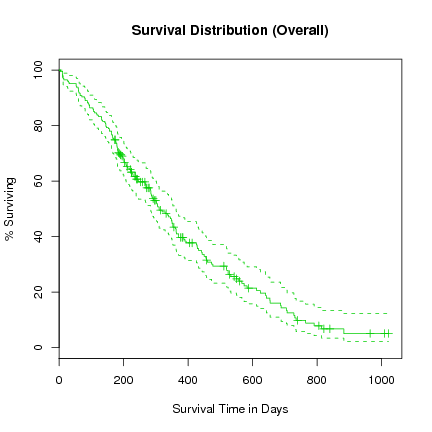
We notice in this plot that the confidence interval is a lot tighter around the fitted survival curve.
We can now add terms to the right side of the formula to group the data by those variables, and view any differences in survival according to the groups:
> l.survfit <- survfit(l.Surv ~ sex, data=lung) > print(l.survfit) |
Call: survfit(formula = l.Surv ~ sex, data = lung)
records n.max n.start events median 0.95LCL 0.95UCL
sex=1 138 138 138 112 270 212 310
sex=2 90 90 90 53 426 348 550
|
> plot(l.survfit, xlab="Survival Time in Days", ylab="% Surviving",
lty=1:2, col=3:4, yscale=100, conf.int=TRUE,
main="Survival Distribution by Gender")
> lines(l.survfit, lty=1:2, lwd=2, cex=2, col=3:4)
> legend("topright", title="Gender", c("Male", "Female"), lty=1:2, col=3:4, lwd=2)
|
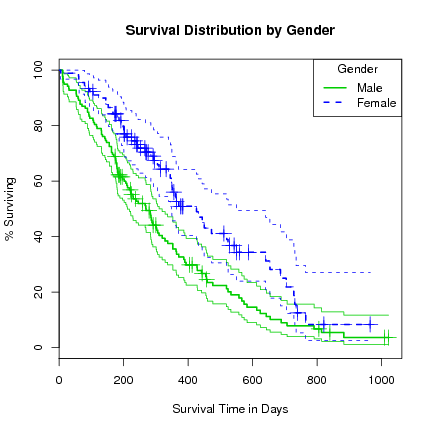
Note that adding further variables to the formula takes a lot longer, and after about 5 variables we risk running out of memory. We can see why since for numeric data each value is ``multiplied'' out (in the sense of a join) and hence exponential growth. Constructing such groups makes little sense.
Test for differences between the two groups (male and female) using a log-rank test (the default):
> survdiff(l.Surv ~ sex, data=lung) |
Call:
survdiff(formula = l.Surv ~ sex, data = lung)
N Observed Expected (O-E)^2/E (O-E)^2/V
sex=1 138 112 91.6 4.55 10.3
sex=2 90 53 73.4 5.68 10.3
Chisq= 10.3 on 1 degrees of freedom, p= 0.00131
|
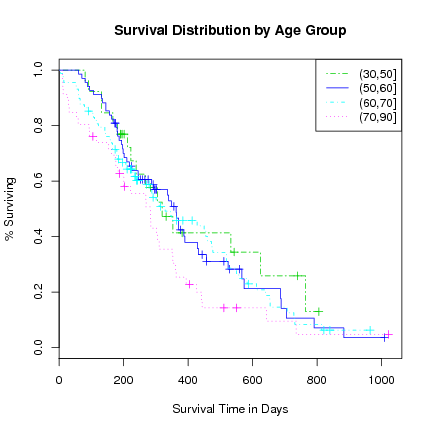
Look at age group survival distributions.
> agecat <- cut(lung$age, c(30, 50, 60, 70, 90)) > l.survfit <- survfit(l.Surv ~ strata(agecat), conf.type="log-log") > print(l.survfit) |
Call: survfit(formula = l.Surv ~ strata(agecat), conf.type = "log-log")
records n.max n.start events
strata(agecat)=agecat=(30,50] 26 26 26 16
strata(agecat)=agecat=(50,60] 68 68 68 48
strata(agecat)=agecat=(60,70] 88 88 88 63
strata(agecat)=agecat=(70,90] 46 46 46 38
median 0.95LCL 0.95UCL
strata(agecat)=agecat=(30,50] 320 223 624
strata(agecat)=agecat=(50,60] 363 245 429
strata(agecat)=agecat=(60,70] 329 239 460
strata(agecat)=agecat=(70,90] 283 176 310
|
> survdiff(l.Surv ~ agecat, rho=0) |
Call:
survdiff(formula = l.Surv ~ agecat, rho = 0)
N Observed Expected (O-E)^2/E (O-E)^2/V
agecat=(30,50] 26 16 20.6 1.0191 1.1749
agecat=(50,60] 68 48 52.0 0.3132 0.4604
agecat=(60,70] 88 63 64.7 0.0437 0.0726
agecat=(70,90] 46 38 27.7 3.8291 4.6404
Chisq= 5.2 on 3 degrees of freedom, p= 0.154
|
> plot(l.survfit, xlab="Survival Time in Days", ylab="% Surviving",
main="Survival Distribution by Age Group",
lty=c(6, 1, 4, 3), col=3:6)
> legend("topright", levels(agecat), lty=c(6, 1, 4, 3), col=3:6)
|
Copyright © Togaware Pty Ltd Support further development through the purchase of the PDF version of the book.